99久久国语对白精品露脸,一区二区三区视频观看,国产精品美女久久久m

四分位數可以在等式中定義如下:

測量分析中四分位數的應用介紹

用前述的準備時間的樣本的例子，將數據羅列出來：

測量分析中四分位數的應用介紹

第一個四分位數是(n+1)/4或(10+1)/4=2.75。75%的樣本數據位于第二個位置的右側。因為第二個位置的值是31，第三個位置的值是35，所以它們的差值是4。那么第一個四分位數就是34(因為31+(3/4 )× (4) = 31+3 = 34)。這意味著在25%的天數內，準備時間小于或等于34分鐘。

第三個四分位數是3(n+l)/4或3(10+1)/4=8.25。25%的樣本數據位于第八個位置的右側。因為第八個位置的值是44，第九個位置的值仍然是44，所以第三個四分位數是44。這意味著在25%的天數內，準備時間大于或等于44分鐘。

當數據量很大時，手工計算均值、中位數、四分位數等描述性統計量會很麻煩。此時，我們可以使用統計軟件，如Minitab或JMP來幫助我們。表1顯示了由Minitab計算的前一個示例中準備時間的統計數據，而圖1顯示了計算統計數據的JMP。表1和圖1中包含的其他描述性統計數據。

測量分析中四分位數的應用介紹

表1 使用Minitab計算準備時間的描述性統計

測量分析中四分位數的應用介紹

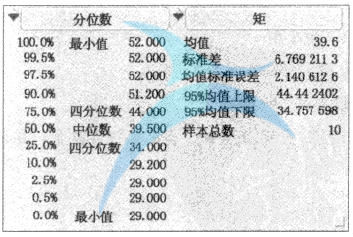
圖1 使用JMP計算準備時間的描述性統計量

測量分析中四分位數的應用介紹

圖2 使用JMP計算完成時間的描述性統計量

現在我們可以檢查上面例子中的描述性統計。表2顯示了Minitab獲得的時間數據的描述性統計。圖2顯示了JMP的計算結果。

從表2和圖2中，我們可以看到69.637和69.5這兩個平均值非常接近。平均值為69.5意味著在一半的情況下，準備時間小于或等于69.5。第一個四分位數代表25%的病例，準備時間小于等于62.35。第三四分位數代表75%的病例，準備時間小于等于76.75。我們也可以知道最快完成時間是46.8分鐘，最慢完成時間是101.1分鐘。

測量分析中四分位數的應用介紹