二項分布有四個特征，如表1所示：
表1 二項分布的特征
服務窗口處理訂單的準確性是快餐店的一個重要質量性特征。每個月美食雜志都會發表其調查結果。準確性是通過由主食、副食和飲料(但遺漏了一個標準食品，如一份泡菜)組成的訂單的準確完成的比例來度量的。假設在最近的一個月，麥當勞里此類訂單準確完成的比例大概是90%。假設你和兩個朋友去麥當勞的服務窗口，每個人要了一份剛剛提到的搭配，如果滿足以下條件時，快餐訂單完成情況數據會滿足二項分布：
1、有一組固定數目的觀察值(你朋友的3份訂單)；
2、每一個觀察值都被歸于兩類中的一類(正確的快餐訂單或不正確的快餐訂單)；
3、一個訂單的結果與其他任何訂單結果是相互獨立的。
為了計算3個快餐訂單里有2個準確訂單的概率，參考表1得到8個可能結果，有3種方式來得到2個正確事件(本例中是兩個準確的快餐訂單)：
可以得出對于給定數目為n的觀察，某一特定數目的事件發生(X)的概率等式。通過將得到在3個快餐訂單里正確訂單方式的個數(1個不正確訂單)，乘以在3個快餐訂單里具有某一具體順序的兩個正確訂單的概率。
從以上，對3個快餐訂單，有3種方式得到2個正確訂單。3個訂單里，以一個特定的順序出現2個正確訂單(如正確-正確-不正確)的概率是：
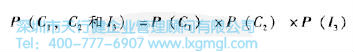
如果P=準確快餐訂單的概率=0.90，那么(1-P)等于一個不準確訂單的概率=0.10。那么：
3×0.081=0.243，為3個快餐訂單里有兩個是準確的概率。對于任何的概率值P和任何樣本大小n，都可以做類似的推導。隨機式(圖3)展現了計算任何二項分布的一般公式。然而，隨著樣本空間的增大，這樣的計算會變的復雜，可以使用Minitab或JMP來代替。圖2為用Minitab對于快餐訂單的計算。
圖2 Minitab二項分布計算
圖3 二項分布等式
從圖2觀察到零個準確快餐訂單的概率是0.001, 1個準確快餐訂單的概率是0.027, 2個準確快餐訂單的概率是0.243，3個準確快餐訂單的概率是0.729。
上一篇:概率的分布
下一篇:如何利用泊松分布計算概率
全國服務熱線：
400-777-6907
天行健企業管理顧問有限公司 全國服務熱線：400-777-6907
郵箱：zyg@leanchina.cn 網址：www.4006801366.com
關注天行健微信
既獲取更多信息
版權所有@深圳市天行健企業管理顧問有限公司 粵ICP備13011693號
