99在线精品视频免费观看软件,国产在线视频一区二区,91精品91久久久久久

正態分布也用于測量數據的連續鐘形分布。連續分布與二項式分布、泊松分布等離散分布在以下幾個方面不同:

1.可變區間范圍內的任何值都可能出現，而不僅僅是一些特定的值(如整數值)。比如循環時間精確到小數點后多少位合適；

2.特定X值出現的概率為零。例如，隨著小數點右邊位數的增加，循環時間被測量為3.000 000 000秒的概率更接近于零；

3.概率可以通過計算曲線下的累計面積來計算。例如，如果曲線已知且穩定，則可以知道周期時間在2.00到3.00分鐘之間的概率。

正態分布用于表示一系列連續數據(變量或CTQ、CTP等。).許多自然現象，如完成一項活動的周期時間、測量誤差、工業產品的尺寸、電壓輸出等。，被發現符合正態分布。圖1描述了正態分布。此外，統計推斷還使用了正態分布。

什么是正態分布？

圖1 正態分布

二、正態分布特性

表1描述了正態分布的一些重要理論性質。

什么是正態分布？

表1 正態分布的特征

正態分布曲線下的概率，可以通過使用正態分布表或者使用Minitab或JMP來計算。圖2說明了在正態曲線下如何查找概率或區域。

什么是正態分布？

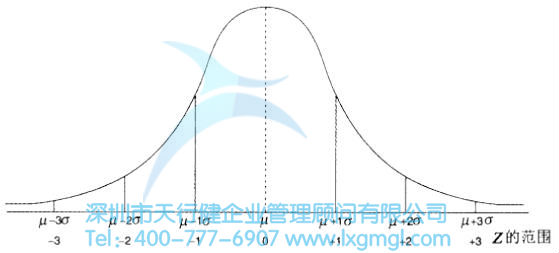
圖2 標準正態分布

第一，通過使用表2可以查找一個值在均值下面少于3個標準差(-3σ)的概率，而表2則是截取于表3的完整正態分布表。

什么是正態分布？

表2 查找-3標準差的累計區域

什么是正態分布？

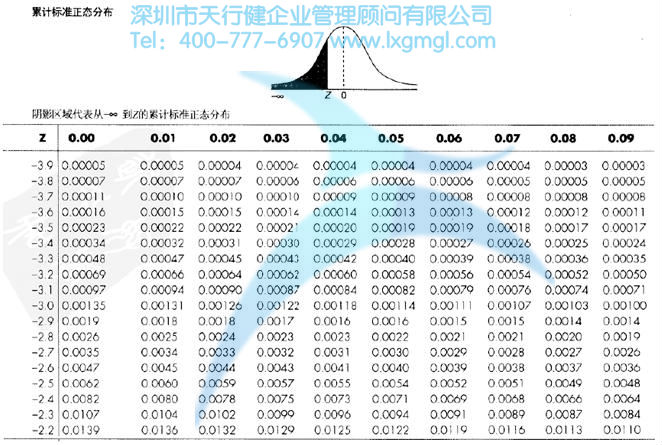
表3 累計標準正態分布

從表2中看出，一個值在一3.00個標準差單元(或Z)下的概率為0.00135或0.135%。

可以計算一個值在均值上面少于三個標準差(+3σ)的概率。表2截取于表3的完整正態分布表，其顯示了在+3.00標準差(或Z)單元下的區域。

什么是正態分布？

表4 查找在+3標準差下的累計區域

從表4可以計算出，一個值小于平均值以上三個標準差(+3σ)的概率為0.99865或99.865%。一個值高于平均值三個標準差(或z)的概率的補數是一個值低于平均值三個標準差(或z)的概率，如圖3所示。

什么是正態分布？

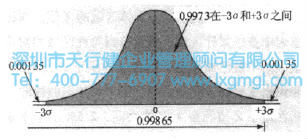
圖3 計算在正態曲線下的區域或概率

因此，一個值超過三個標準差單位(或z)的概率為1.0-0.99865=0.00135。注意+3σ以上的面積與-3σ以下的面積相同。這是因為正態分布是對稱的，所以曲線的每一半都是另一半的鏡像。在平均值之外，大于三個標準差的面積等于或小于-3σ(0.00135)的面積和+3σ(0.00135)的面積之和。等于0.00135+0.00135=0.0027或0.27%。另一種表達是:一萬次中有27次機會，一個值會大于平均值之外的三個標準差。這個表達式的補充是，有1-0.0027=0.9973或99.73%的概率，一個值在平均值的三個標準偏差之內。表5總結了一些不同標準偏差單位的信息。

什么是正態分布？