国产一级片播放,日韩av成人女同恋,毛片毛片

為了理解區間估計的概念，讓我們回到網站訂單完成時間的200個例子。討論繪制測量數據圖表的順序，“在圖表中顯示數據”。現在把這200單的完成時間看成一個整體，整體的特點在實際情況中是未知的。對于這一人群，平均值為69.637分鐘，標準偏差為10.411分鐘。

為了測試不同樣本之間的差異，從總共200個訂單中選擇樣本空間n為10的20個不同樣本。這些樣品的結果如表1所示。

置信區間的基本概念

從表1中，我們可以得出以下結論:

1.不同樣本的樣本統計是不同的。樣本均值在61.10分鐘至76.26分鐘之間變化，樣本標準差在6.50分鐘至14.10分鐘之間變化，樣本中值在61.35分鐘至76.85分鐘之間變化，樣本范圍在21.50分鐘至41.60分鐘之間變化。

2.部分樣本平均值大于總體平均值69.637分鐘，部分樣本平均值小于總體平均值；

3.部分樣本的標準差大于總體標準差10.411分鐘，部分樣本的標準差小于總體標準差。

4.不同樣本的變異遠遠大于樣本的標準差。

不同樣本之間樣本統計量的差異稱為抽樣誤差。抽樣誤差是從總體中選擇單個樣本時的變化。抽樣誤差的大小主要取決于總體的變異程度和樣本量。大樣本認為對于小樣本，采樣誤差較小但成本較高。

因為在實踐中通常只選擇一個樣本，統計學家開發了一些有特色的方法來估計人口，包括由上限和下限組成的區間，而不是一個值。這個區間稱為置信區間估計。使用表1中的訂單完成時間來說明總訂單完成時間平均值的置信區間估算，如表2所示，20個樣本，每個n為10:

置信區間的基本概念

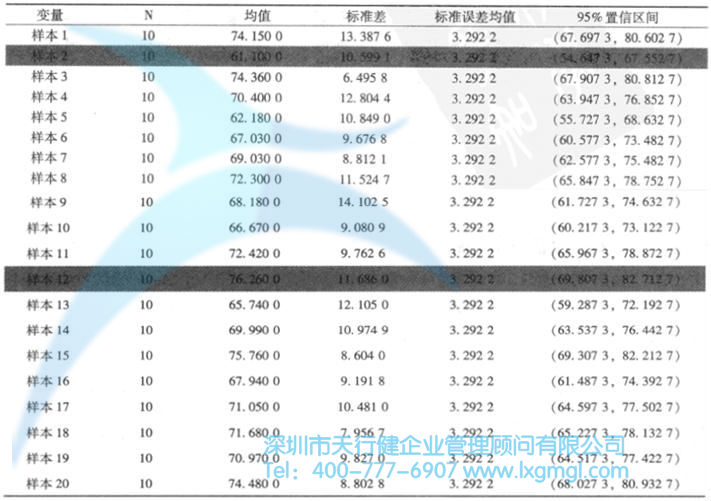
首先，檢查第一個選定的樣本。樣本均值為74.15分鐘，樣本標準差為13.3876分鐘，總體均值的區間估計為67.6973-80.6027分鐘。我們不需要知道這個置信區間估計值是否準確，因為在實際研究中我們很少知道總體均值的實際大小。然而，在訂單完成時間的例子中，已知整體平均值為69.637分鐘。如果我們檢查67.6973-80.6027分鐘的區間，我們會發現69.637的整體平均值包含在這個區間內。因此，第一個樣本以區間估計的形式準確地估計了總體均值。再看其他19個樣本，我們會發現除了第二個和第十二個樣本之外，所有的樣本都有類似的結果。對于對應于每個樣本的區間(除了第2個和第12個樣本)，69.637的總平均值落在區間的某處。

但對于第二個樣本，平均樣本為61.10分鐘，間隔為54.6473-67.5527分鐘，對于第十二個樣本，間隔為69.8073-82.7127分鐘。樣本平均值69.637落在區間外，用這兩個樣本對總體平均值的估計是不準確的。

實踐中，使用區間估計主要存在兩個問題:實踐中只選取一個樣本，無法100%確定總體特征的估計是正確的；然而，通過將確定水平設置為小于100%的值，并使用總體特征的區間估計，我們可以基于給定的精度獲得統計推斷。

通常，95%的置信區間估計值可以理解為，如果選擇了所有可能的n尺寸樣本，則95%的樣本將包括整體特征，5%的樣本將不包括整體特征。

95%是最常用的置信區間，如果需要增加置信度的話。99%也是常用的。如果你需要更少的自信，你可以用90%。然而，不同的置信水平和置信區間 width之間有得有失。對于給定的樣本量，如果您希望置信區間具有更高的置信度以包含整體特征，則置信區間會更寬，采樣誤差也會更大。

無論估計人口的哪個特征，置信區間估計的基本概念都是一樣的。為了執行置信區間估計，我們需要知道用于估計總體特征的樣本統計及其抽樣分布。