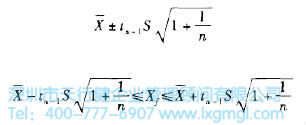
除了總體平均值的置信區間估計之外，通常還需要預測未來個體值的結果。
雖然平均預測區間的形式與置信區間估計相似，但對預測區間的理解是不同的。預測區間是對可觀察的未來個體值X1的估計，而不是對未知總體參數μ的估計。因為Minitab和JMP現在無法計算預測區間，所以預測區間如公式1所示:
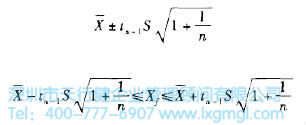
式1
回到保險申請處理時間的例子（在此《均值的置信區間估計(σ未知)》文章）中來，假設我們未來需要建立個人保險申請處理時間95%的預測區間估計。使用公式2:
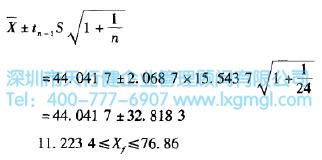
式2
因此，我們預測未來個人保險申請的辦理時間為11.22-76.86天，概率為95%。這個結果明顯不同于均值的置信區間估計。因為我們估計的是未來的個人價值，而不是整個人口的平均值，所以預測區間足夠寬。
2.比例的置信區間估計
因子的置信區間估計可用于估計給定類別中事件的概率。樣本均值可以用來估計總體均值，這里我們可以利用事件的樣本比例(P)來估計總體比例(π)。
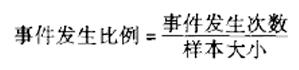
樣本統計量p服從二項分布，在大多數情況下可以用正態分布來近似。
為了說明比例的置信區間估計，我們可以考察大城市報紙質量工程師面臨的問題。在報紙生產過程中，一個重要的質量特征與印刷報紙的比例有關，盡管存在許多不一致的因素，如印刷過剩、頁面設置不合理、缺頁或多頁等。因為測試每份報紙是不現實的(耗時且昂貴)，所以隨機抽取了200份報紙作為研究和使用的樣本。假設有35個樣本，容量為200，在某種程度上質量問題最多。下表是Minitab對存在質量問題的報紙比例的95%置信區間估計:
因此，所有置信區間的95%來自200份報紙的隨機樣本，這將包括總體比例。由于總比例未知，12.2% ~ 22.8%的區間可能是包含總比例的95%的區間，而建立無總比例區間的概率為5%。
對于給定的樣本量，比例的置信區間通常比其他測量變量更寬。對于連續變量，通過測量其概率獲得的信息比分類變量獲得的信息多。換句話說，分類變量只有兩個可能的值，這與連續變量的概率度量相比是粗略的。因此，分類變量的測量只能為估計的參數提供很少的信息。
上一篇:均值的置信區間估計(σ未知)
下一篇:如何進行流程圖分析
全國服務熱線：
400-777-6907
天行健企業管理顧問有限公司 全國服務熱線：400-777-6907
郵箱：zyg@leanchina.cn 網址：www.4006801366.com
關注天行健微信
既獲取更多信息
版權所有@深圳市天行健企業管理顧問有限公司 粵ICP備13011693號
