国产女教师bbwbbwbbw,日韩精品免费一区二区三区竹菊,亚洲中文无码一区二区三区

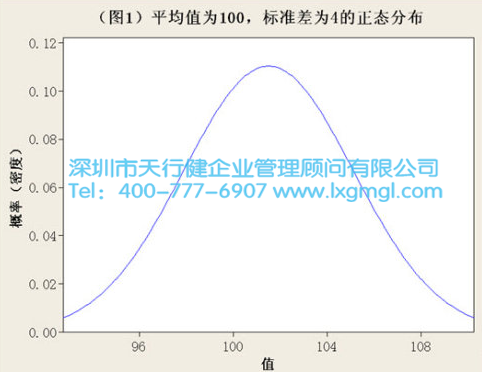
在管理活動中最常遇到的連續分布是正態分布，也稱為高斯分布，用于描述隨機變量(如月銷售額)的值的規律性。從理論上可以證明，如果一個指標受到許多隨機因素的干擾或影響，并且每個干擾或影響都很小，那么所有干擾影響的綜合結果將導致該指標呈正態分布。圖1顯示了平均值為100、標準偏差為3的正態分布。天行健咨詢指出，在實際操作中，你會經常發現其他均值和標準差不同的正態分數看起來和下圖差不多，唯一的區別就是曲線底部的跨度不同。

服務類六西格瑪的獨特技術挑戰--非正態數據處理戰略

正態分布是常用統計分析工具的基礎，因為大多數統計分析工具的前提是數據服從正態分布，統計分析工具有效性的關鍵取決于這一假設的真實性。如過程能力分析、方差分析、T檢驗、標準回歸分析、置信區間、控制圖等。實際數據不服從正態分布，我們不知道數據分布偏斜的原因。我們做什么呢

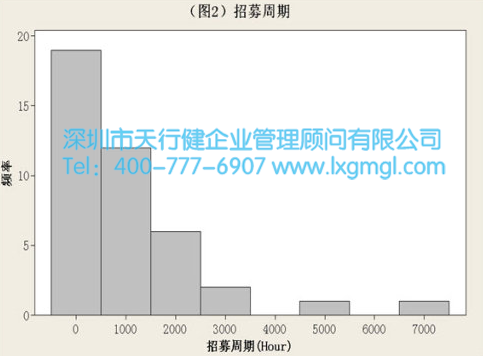
圖2是人力招聘周期的數據，即從招聘需求填寫時間到招聘時間的數據。這些數據與圖1中的數據完全不同。它們可以被稱為“右傾”，因為它們是傾斜的(不對稱的)，分布高度沿橫軸逐漸降低。這種數據在非制造業領域很常見。在這種情況下，數據分布趨勢是傾斜的，因為不會出現負的招聘時間。

服務類六西格瑪的獨特技術挑戰--非正態數據處理戰略

非正態數據趨勢往往以其他方式出現，比如把一個從1到10的測量水平作為連續變量。在這種情況下，數據應該是離散的。因為只能得到10個獨立值，所以數據不能遵循連續正態分布。

所以，如果很多統計分析工具采用正態分布，而周期測量等非制造領域的數據往往是偏態的，那是不是意味著你不能在這類情況下應用統計分析工具呢？乍一看，這是一個合理的假設，不幸的是，很多六西格瑪提供商和顧問已經教過這個問題了。實際上，情況并非如此。我們可以應用標準的統計分析工具，但必須有更深入的技術理解才能決定如何應用。為了說明如何做到這一點，我們將詳細介紹正態分布和正態假設，然后討論如何分析異常數據。

要理解的最重要的原理是，正態分布是一個概念模型，即理論上存在，現實中不存在。所以，真正要回答的問題不是數據是否服從正態分布(他們不能！)，而是數據是否近似正常。說正態分布實際上并不存在可能會讓人覺得奇怪，但是仔細分析正態分布就很明顯了。

上面的圖1顯示了理論上的正態分布覆蓋了從負無窮大到正無窮大，也就是說，沒有最大值和最小值。所以現實中的數據如果要服從這種分布，其最大最小兩端都不會有邊界，這在現實中是不可能的。如果時間是一個關鍵的質量特性，你無法觀察到負的時間，那么時間就不可能是完全正態分布，類似于金錢等等。在實踐中，你永遠看不到一個完整的正態分布的另一個原因是，連續分布根據定義有無限個可能的結果(數學上，為了精確定義，我們應該說“不可數無窮”)。上面的圖1說明了這一點，其中分布曲線是連續的，沒有中斷。實際上，發生這種情況的唯一方法是，測量具有無限小數位的周期。即使你測完了，轉換到小數點后兩位也不能得到很多值，這樣會打斷分布，技術上稱之為離散分布(統計學家會稱之為“可數無窮”)，再次導致非正態性。

你可能會說這是一個吹毛求疵的論點，但它揭示了為什么現實中沒有一個數據能完全服從正態分布，即正態分布只是一個實際意義上的概念模型。所以真實的數據并不是完全正態的，正態性是很多統計分析工具的前提。在實踐中，不需要完全正態，只需要近似正態。