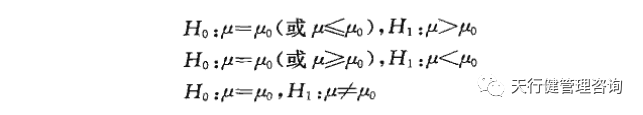
參數估計和假設檢驗是統計推斷的兩個重要方面。參數估計以“數”為輸出結果,假設檢驗以“判斷”為輸出結果。
假設檢驗:根據所獲樣本, 運用統計分析方法對總體X的某種假設做出接受或拒絕的判斷。
在實際工作中,當樣本均值不等于總體均值或樣本均值不等于樣本均值時,應考慮兩種可能:由于采樣錯誤所致;兩者來自不同的總體。如何做出判斷?統計上這個問題是通過假設檢驗來解答。
假設檢驗的步驟可以總結如下:
(1)建立假設。假設檢驗的第一步是建立假設,通常需要建立兩個假設:原假設H0和備選假設H1。
對總平均值執行檢驗時,有三種類型的假設:
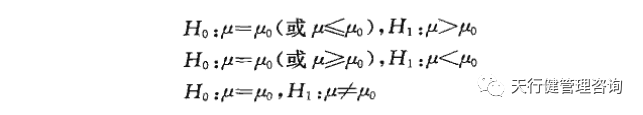
前兩個是單邊假設檢驗,第二個是雙邊假設檢驗。假設檢驗的任務是根據樣本x1、x2、…、xx判斷原來的假設是否為真。
(2)選擇檢驗統計,確定拒收域的形式。如果總體的平均值為檢驗,則樣本平均值x用于導出檢驗統計量;如果正態總體的方差為檢驗,則從樣本方差s2中導出檢驗統計量。
根據統計量的值,整個樣本空間分為拒絕域W和非拒絕域a兩部分,當樣本統計量的值落在拒絕域時,原假設被拒絕,否則原假設不能被拒絕。因此,被拒絕的域必須在假設檢驗中找到。
根據可選的假設,拒絕域可以是雙邊的或單邊的。在確定了拒絕域的類型后,還應確定臨界值C,臨界值C應根據允許的錯誤概率來確定。
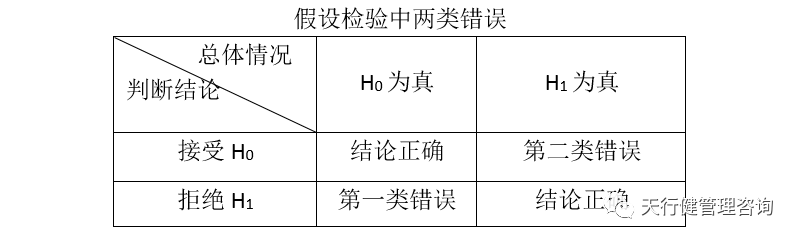
(3)在檢驗中給出顯著性水平a。在判斷原始假設是否為真時,由于樣本的隨機性,判斷中可能存在兩種錯誤,如下表所示。第一種錯誤是當原假設為真時,由于樣本的隨機性,樣本的觀測值落入拒絕域W,從而做出拒絕原假設的決定。其出現的概率稱為做出第一類錯誤的概率,也稱為拒絕真理的概率,記錄為a,即pH (w) =a,第二類錯誤是當原假設為假時,由于樣本的隨機性,樣本的觀測值落入非拒絕域A,從而做出原假設不能被拒絕的判定。其出現的概率稱為犯第二類錯誤的概率,也稱為取假概率,記錄為β,即PH1(A)=β。
如果要求犯第一類錯誤的概率不超過a,由此給出的檢驗稱為水平為a的檢驗,稱a為顯著性水平,通常取0.05,有時也可能取0.10等。
要真正理解假設檢驗結論的含義,就要具體理解犯兩種錯誤的現實意義。
第一種錯誤的解釋:一般來說,H0建立的時候,拒絕了H0,這是第一種錯誤。一般以a=0.05作為犯第一類錯誤的風險概率。
第二種錯誤的解釋:一般來說,當H0失敗時,它沒有拒絕H0,這是第二種錯誤。
(4)給出臨界值,確定拒絕域。有了顯著性水平a,我們就可以根據給定的檢驗統計量分布,查表得到臨界值,從而確定具體的拒絕域。在假設的不同替代下,拒絕域、臨界值和顯著性水平a的關系不同,其示意圖如下圖所示。
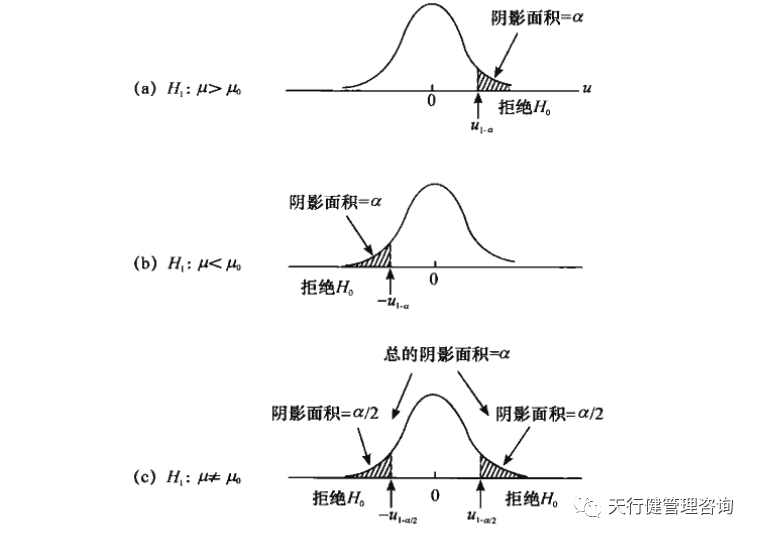
備擇假設、拒絕域和顯著性水平
(5)根據樣本的觀測值,計算檢驗統計量的值。收集樣本數據,計算檢驗統計值。
(6)根據檢驗統計量的值是否屬于拒絕域進行判斷。
1)將檢驗統計量的值與拒絕臨界值進行比較,當其落入拒絕域時,做出拒絕原假設的結論,否則,做出不能拒絕原假設的結論。
2)根據檢驗統計量計算P值。p是原假設成立時當前形勢的概率(嚴格來說是當前形勢或更不利形勢對原假設的概率,即原假設成立時對備選假設更有利的形勢)。當這個概率很小(例如小于0.05)時,在原假設成立的情況下,這個結果不應該出現在實驗中。但現在確實出現了,所以有理由認為“原假設成立”的前提是錯誤的,所以我們應該拒絕原假設而接受替代的假設。所以有一個普遍規律:如果P<a,則拒絕原假設。目前大多數統計軟件都提供了與假設檢驗對應的P值,不必再查統計表確定拒絕域就可以根據P值做出判斷。
3)根據樣本的觀測值,可以得到總體參數的置信區間。如果原假設的參數值不落入該置信區間,則做出拒絕原假設的結論,否則作出保留原假設的結論。目前大多數統計軟件都提供了相應的置信區間,不需要自己計算,所以用這種方法判斷也很方便。
如果總體平均值為假設檢驗,用戶通常會提前指定顯著性水平,以確定第一類錯誤的概率。在此基礎上,通過控制樣本量,也可以控制第二類誤差的概率。以下描述了如何在總平均值的單側檢驗中確定樣本量。
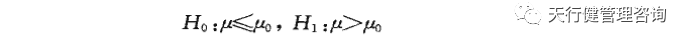
式中,μ0為原假設總體均值。
由于兩類錯誤造成的損失類型不同,嚴重程度不同,不同的人對兩類錯誤發生的概率可能會做出不同的限制。但是,在確定樣本量之前,必須明確定義兩種類型錯誤的允許概率。
在假設檢驗中,經常使用一個名詞:探測能力。它的定義是1-β,相當于備選假設成立時不犯第二類錯誤的概率,或者備選假設成立時拒絕原假設的概率。

1.單樣本Z檢驗;
2.單樣本t檢驗;
3.雙樣本t檢驗;
4.成對t檢驗;
5.單比例檢驗;
6.雙比例檢驗;
7.雙樣本方差假設檢驗;
單樣本Z檢驗/t檢驗:計算連續單樣本總體均值或均值的假設檢驗的置信區間。
單個樣本Z檢驗:
用于計算單個樣本總體均值的置信區間,或當總體標準差已知時均值的假設檢驗。 當樣本量大于30時,通常使用單樣本Z檢驗。
單樣本t檢驗:
用于在總體標準差未知的情況下,計算連續單樣本總體均值或均值的假設檢驗的置信區間。 當樣本量小于或等于30時,通常使用單樣本t檢驗。
雙樣本t檢驗:計算來自不同總體均值和總和假設檢驗的兩個連續樣本的置信區間。
當總標準偏差未知時使用; 從不同總體均值計算兩個樣本的置信區間,并進行假設檢驗。
成對t檢驗:
當兩組數據成對出現時使用(即在不同條件下連續兩次測量同一種群得到的數據); 計算兩對數據平均值的置信區間或進行假設檢驗。
單比例檢驗:對單個比例進行假設檢驗和置信區間的計算。
雙比例檢驗:對兩個比例間的差異進行假設檢驗和置信區間的計算。
雙樣本方差假設檢驗:可以進行兩個樣本總體方差的假設檢驗和置信區間的計算。
上一篇:六西格瑪,能用于餐館么?